Inferring a good phylogenetic tree topology, i.e. a tree without branch lengths, is the primary challenge for efficient tree inference. As such, we and others think a lot about how algorithms move between topologies, typically formalizing this information as a path through a graph representing tree topologies as vertices and edges as moves from one tree to another. Removing all branch length information makes sense because algorithms are formulated in terms of these topologies: for classical unrooted tree inference, the set of trees that are tried from a specific tree is not determined by the branch lengths of the current tree.

But what about time-trees? Time-trees are rooted phylogenetic trees such that every event is given a time: each internal node is given a divergence time, and each leaf node is given a sampling time. These are absolute times of the sort one could put on a calendar. To first approximation, working with time-trees is synonymous with running BEAST, and we are indebted to the BEAST authors for making time-trees a central object of study in phylogenetics. Such timing information is essential for studying demographic models, and in many respects time-trees are generally the “correct” tree to use because real evolution does happen in a rooted fashion and events do have times associated with them.

Because timing is so central to the time-tree definition, and because it’s been shown that defining the discrete component of time-tree moves with reference to timing information works well, perhaps we shouldn’t be so coarse when we discretize time-trees. Rather than throw away all timing information, an alternative is to discretize calendar time and have at most one event per discretized time. If we have the same number of times as we have events on the tree, this is equivalent to just giving a ranking, or total order, on the events in the tree which is compatible with the tree structure. One can be a little less coarse still by allowing branch lengths to take on an integer number of lengths.

The goal of our most recent preprint is to analyze the space of these discretized time-trees. The study was led by Alex Gavryushkin while he was at the Centre for Computational Evolution in Auckland. Chris Whidden and I contributed bits here and there. As for classical discretized trees, we build a graph with the discretized time-trees as vertices and a basic set of moves on these trees as edges. The goal is to understand basic properties of this graph, such as shortest paths and neighborhood sizes.

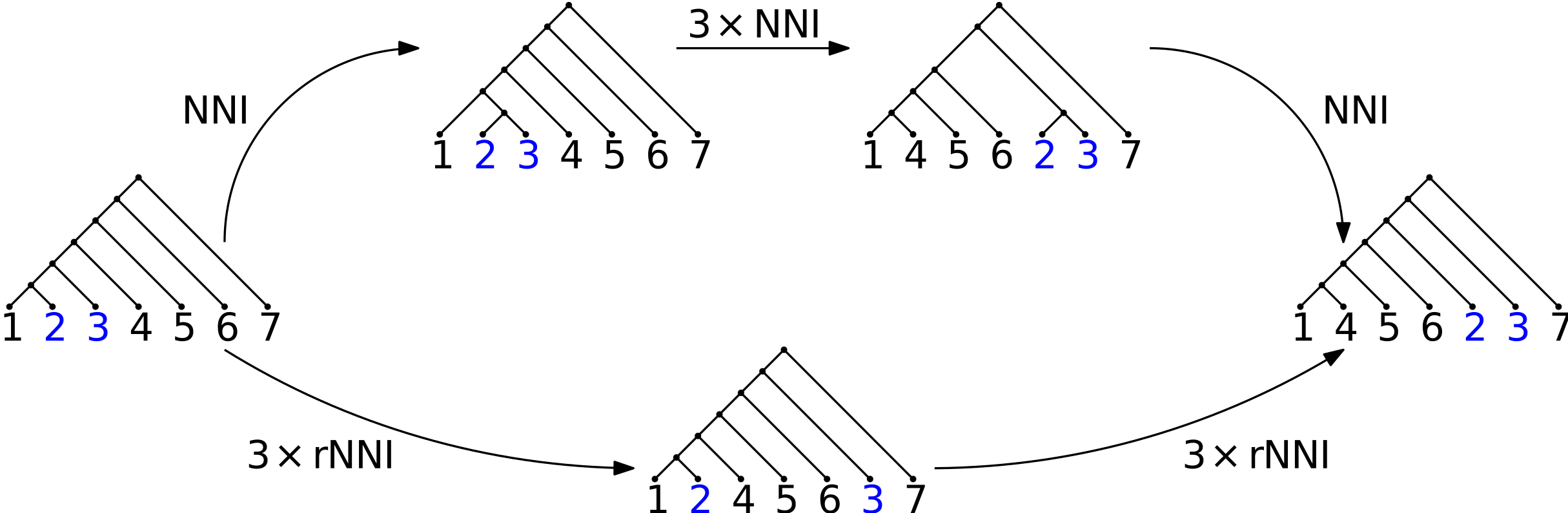
Adding timing information makes a substantial difference in the graph structure. The simplest example of this is depicted above, which compares the usual nearest-neighbor interchange (NNI) with its ranked tree equivalent (RNNI). RNNI only allows interchange of nodes when those nodes have adjacent ranks. The picture shows an essential difference between shortest paths for NNI and RNNI: if one would like to move the attachment point of two leaves a good ways up the tree, it requires fewer moves to first bundle the leaves into a two-taxon subtree, move that subtree up the tree, then break apart the subtree. On the other hand, for RNNI, a shortest RNNI graph path simply moves the attachment points individually up the tree. This is an important difference: for example, the computational hardness proof of NNI hinges on the bundling strategy resulting in shorter paths.

The most significant advance of the paper is the application of techniques from a paper by Sleator, Trajan, and Thurston to bound the number of trees in arbitrary diameter neighborhoods. The idea is to develop a “grammar” of transformations such that every tree in a neighborhood with a given radius k can be written as a word of length k in the grammar. Then, the number of trees in the neighborhood is bounded above by the number of letters to the power of the word length. Further refinements lead to some interesting bounds. In an interesting twist, these neighborhood size bounds provide a generalized version of a counter-example like that shown in the figure, which shows in more generality that the arguments for the computational hardness proof of NNI do not hold.

Some very nice work from Alex. There’s going to be more to this story– stay tuned!