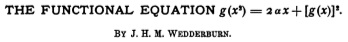In the upcoming special issue on phylogenetics in Algorithms for Molecular Biology, Steve Evans and I have a paper showing that the “obvious” ways to algebraically characterize the shape of a phylogenetic tree do not uniquely identify the tree with probability going to one as the number of leaves goes to infinity. Specifically, we investigate the spectrum of the pairwise distance, adjacency, and Laplacian matrices, as well as generalizing these conclusions about the spectrum to the case of immanantal polynomials. As part of it, we adapt a beautiful 1921 argument of Wedderburn to show that the number of rooted bifurcating trees that do not contain a given subtree is asymptotically smaller than the total number of such subtrees.