We are equipped with purpose-built molecular machinery to mutate our genome so that we can become immune to pathogens. This is truly a thing of wonder.

More specifically, I’m talking about mutations in B cells, the cells that make antibodies. Once a randomly-generated antibody expressed on the outside of the B cell finds something it’s good at binding, the cell boosts the mutation rate of its antibody-coding region by about one million fold. Those that have better binding are rewarded by stimulation to divide further. The result of this Darwinian mutation and selection process is antibodies with improved binding properties.

The mutation process is wonderfully complex and interesting. Being statisticians, we payed our highest tribute that we can to a process we think is beautiful: we developed a statistical model of it. This work was led by the dynamic duo of Jean Feng and David Shaw, while Vladimir Minin, Noah Simon and I kibitzed. Our model is known in statistics as a type of proportional hazards model. These models were introduced in Sir David Cox’s paper Regression Models and Life-Tables, which with over 4600 citations makes it the second most cited paper in statistics.

These models are typically used to infer rates of failure, such as that of humans getting disease. During our life span we get a sequence of diseases, some of which predispose us to other diseases. By considering sequences of diseases across many individuals, we can use these proportional hazards models to infer the rate of getting various diseases given disease history.

There is an analogous situation for B cell sequences in that the mutation process depends significantly on the identity of the nearby bases. We can observe lots of mutated sequences, and do a similar sort of inference: when a position mutates, it changes the mutability of nearby bases. Unfortunately we don’t know the order in which the mutations occurred, and thus don’t know what sequences had increased mutability, so we have to do Gibbs sampling over orders. The paper describing these methods and some results is published in Annals of Applied Statistics.

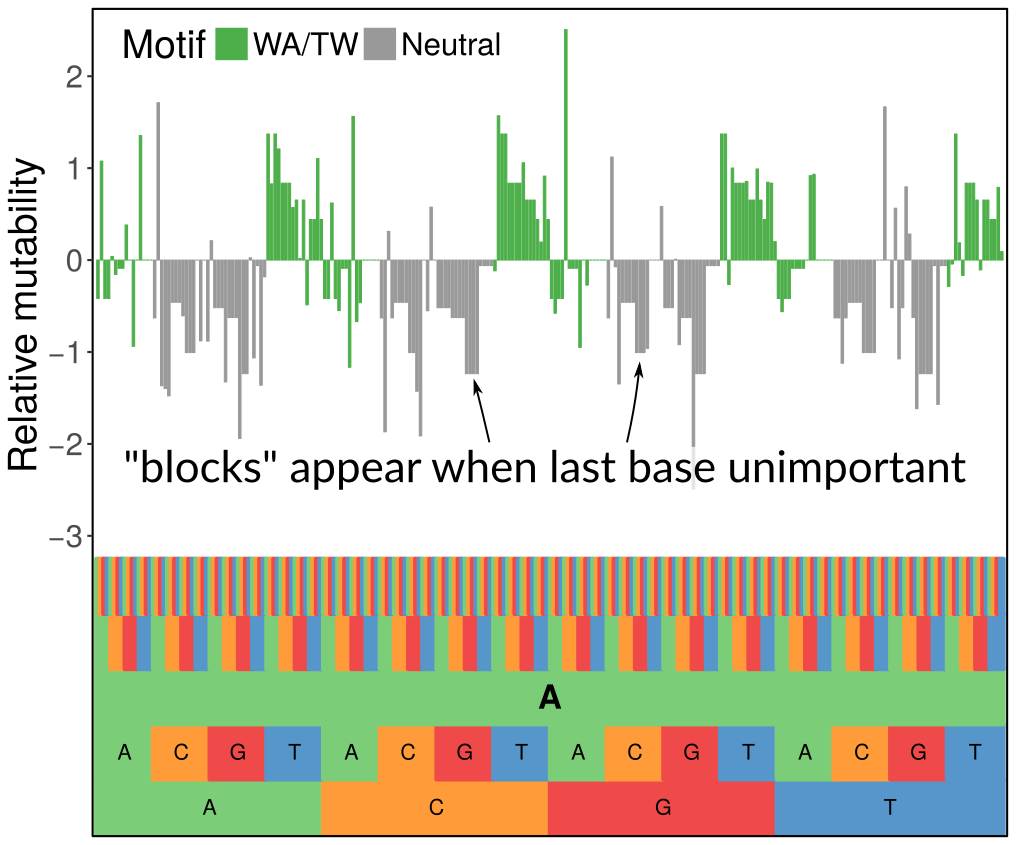
We were inspired by the very nice work of the Kleinstein lab developing similar sorts of models using simpler methods. However, we wanted a more flexible modeling framework and for the complexity of the models to automatically scale to the signal in the data, which we did using penalization with the LASSO. What you see in the figure above is how we can set up a hierarchical model with a penalty that zeroes out 5-mer terms when they don’t contribute anything above the corresponding 3-mer term (the last base being unimportant gives the block-like structure, while when the first base is unimportant it gives the 4-fold repetitive pattern you can see when zooming out). We are also indebted to Steve and his team, especially Jason Vander Heiden, for supplying us with sequence data. They are a class act.

There’s a lot of interest in context-sensitive mutation processes these days, such as Kelly Harris’ work on how we can watch context-sensitive mutabilities change through evolutionary time, and Ludmil Alexandrov’s work on mutation processes in cancer. In both of these cases, they are in the process of transitioning from a statistical description of these processes to linking them with specific mutagens and repair processes.

Here too we would like to use statistics to learn more about the mechanisms behind these context-sensitive mutations. What’s neat about the framework that Jean and David developed is that now we can design features that correspond to specific mechanistic hypotheses and test how much they impact mutation rates. Stay tuned!